Tests of Big Bang: Expansion

Edwin Hubble

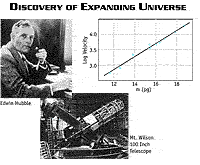
The Big Bang model was a natural outcome of Einstein's General Relativity as applied to a homogeneous universe. However, in 1917, the idea that the universe was expanding was thought to be absurd. So Einstein invented the cosmological constant as a term in his General Relativity theory that allowed for a static universe. In 1929, Edwin Hubble announced that his observations of galaxies outside our own Milky Way showed that they were systematically moving away from us with a speed that was proportional to their distance from us. The more distant the galaxy, the faster it was receding from us. The universe was expanding after all, just as General Relativity originally predicted! Hubble observed that the light from a given galaxy was shifted further toward the red end of the light spectrum the further that galaxy was from our galaxy.

The Hubble Constant

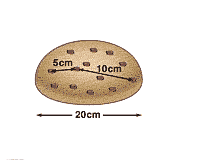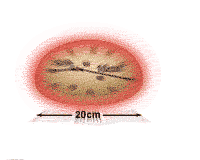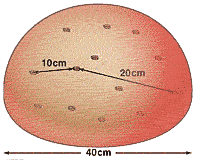The specific form of Hubble's expansion law is important: the speed of recession is proportional to distance. Hubble expressed this idea in an equation - distance/time per megaparsec. A megaparsec is a really big distance (3.26 million light-years). The expanding raisin bread model at left illustrates why this proportion law is important. If every portion of the bread expands by the same amount in a given interval of time, then the raisins would recede from each other with exactly a Hubble type expansion law. In a given time interval, a nearby raisin would move relatively little, but a distant raisin would move relatively farther - and the same behavior would be seen from any raisin in the loaf. In other words, the Hubble law is just what one would expect for a homogeneous expanding universe, as predicted by the Big Bang theory. Moreover no raisin, or galaxy, occupies a special place in this universe - unless you get too close to the edge of the loaf where the analogy breaks down.

The current WMAP results show the Hubble Constant to be 71.0 ± 2.5 (km/sec)/Mpc. If the WMAP data is combined with other cosmological data, the best estimate is 70.4 ± 1.4 (km/sec)/Mpc.